Subgraph Isomorphism

Introduction

Recently while reading a blog post on detecting indirect control flow, I came across the concept of subgraph isomorphism. Here is an introductory blog post covering the problem and a few algorithms related to it.

The subgraph isomorphism problem is the problem of determining whether a graph \(G\) has a subgraph \(G'\) that is isomorphic to a given graph \(P\). Let us formally define a few terms.

Graph: Graph is a data structure consisting of a set of vertices/nodes along with a set of edges that connect a pair of these vertices.

\[ G = (V, E), \quad V = \{v_1, v_2, \dots, v_n\}, \quad E \subseteq V \times V \]

Degree: Degree of a vertex/node is the number of edges connected to it.

Adjacency Matrix: The adjacency matrix of a graph \(G = (V, E)\) with \(|V| = n\) vertices is an \(n \times n\) matrix \(A = [a_{ij}]\), where each element \(a_{ij}\) indicates whether an edge exists between vertices \(v_i\) and \(v_j\).

\[ a_{ij} = \begin{cases} 1, & \text{if } (v_i, v_j) \in E, \\ 0, & \text{otherwise.} \end{cases} \]

Subgraph: A graph \(G'\) is called a subgraph of \(G\) if every vertex and edge of \(G'\) is contained in \(G\) \[ G' = (V', E') \]

\[ \textit{where } V' \subseteq V \textit{ and } E' \subseteq E. \]

Induced Subgraph: A subgraph is said to be induced if it preserves all the edges that exist between its vertices in the original graph.

\[ G' = (V', E'), \quad V' \subseteq V, \quad E' = E \cap (V' \times V') \]

Isomorphism: Two graphs are said to be isomorphic if there exists a one-to-one correspondence between their vertices that preserves adjacency.

\[ G_1 = (V_1, E_1), \quad G_2 = (V_2, E_2) \]

\[ G_1 \cong G_2 \quad \textit{if there exists a bijection } \phi : V_1 \rightarrow V_2 \textit{ such that } (u, v) \in E_1 \iff (\phi(u), \phi(v)) \in E_2 \]

Subgraph Isomorphism

Subgraph Isomorphism is an NP-complete problem that determines whether a graph has a subgraph that is isomorphic to a given pattern graph. 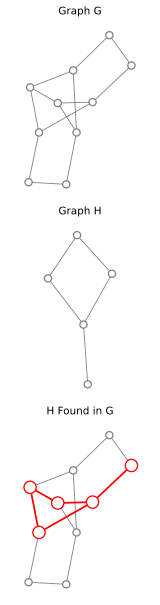Example of Subgraph Isomorphism - from Wikipedia

A neat mathematical formulation of this problem uses matrices -

Consider a pattern graph P and a target Graph G. We want to determine if a subgraph exists within G that is isomorphic to pattern Graph P. It is possible to encode a valid subgraph isomorphism in a \(|V_P| \times |V_G|\) matrix \(M\) where \(|V_P|\) represents the number of vertices in the graph P.

In this matrix, set \(m_{ij} = 1\) if and only if \(v_j \in G\) corresponds to \(v_i \in P\) in the isomorphism. For this matrix to qualify for subgraph isomorphism, it must satisfy two constraints -

  • Each row must contain exactly one 1: This ensures that every vertex in \(P\) is mapped to exactly one vertex in \(G\).
  • Each column must have at most one 1: This ensures that no two vertices in \(P\) are mapped to the same vertex in \(G\).

Given a matrix satisfies these two conditions, we can check if it satisfies subgraph isomorphism using the following inequality

\[ A_P \leq M A_G M^{T} \quad \text{(componentwise)} \]

For induced subgraph isomorphism we use strict equality \[ A_P = M A_G M^{T} \quad \text{(componentwise)} \]

Naive Algorithm

A naive algorithm to find a subgraph isomorphism is to enumerate all possible matrices M and see if it satisfies the inequality.

To start with, we set up a matrix consisting of 1's and 0's to represent all possible mappings between vertices in P and vertices in G. We could initialize M as a matrix of all 1s, meaning “every vertex in P can map to every vertex in G.” However, this would create an enormous search space.

To reduce it, we apply a simple degree-based constraint:

For every possible \(v_i \in P\) being mapped to \(v_j \in G\), \(\deg(v_i) \leq \deg(v_j)\)

This condition ensures that a vertex in P is only mapped to a vertex in G that has at least as many neighbors. If a vertex in P has a higher degree than its image in G, it would be impossible to match all its adjacent vertices correctly, making that mapping invalid.

Once we have constructed the initial matrix M based on the degree constraint, we begin a brute-force search to find a valid mapping. This involves systematically removing extra 1’s from M to generate candidate matrices M' that satisfy the row and column constraints.

For each such candidate M′, we check whether it satisfies the subgraph isomorphism inequality.

If the condition is not satisfied, we generate another valid mapping M′′, and repeat the process until a match is found or all possibilities are exhausted.

Brute Force Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Algorithm (A_G, A_P, M):
    Input: 
        A_G - adjacency matrix of target graph
        A_P - adjacency matrix of pattern graph
        M - initial mapping matrix (based on degree constraints)
    Output:
        True if subgraph isomorphism exists, False otherwise

    return Search(M, 0, [False]*|V_G|, A_G, A_P)


Procedure Search(M, depth, used, A_G, A_P):
    if depth == |V_P|:
        if A_P ≤ M * A_G * Mᵀ:
            return True
        else:
            return False

    // compute candidate columns before mutating M
    candidates = []
    for each column j in A_G:
        if M[depth][j] == 1 and not used[j]:
            append j to candidates

    for each j in candidates:
        rowBackup = copy of row M[depth]
        // set row 'depth' to one-hot at column j
        set all entries in row 'depth' of M to 0
        M[depth][j] = 1
        used[j] = True

        if Search(M, depth + 1, used, A_G, A_P):
            return True

        // backtrack
        used[j] = False
        restore row M[depth] from rowBackup

    return False

Ullmann's Algorithm

Ullmann's algorithm prunes the search space further by applying a neighborhood consistency heuristic. A vertex \(v_i\) in P can only map to \(v_j\) in G only if every neighbor of \(v_i\) in P also has at least one match in the neighbors of \(v_j\) in G.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
Algorithm Ullmann(A_G, A_P):
    Input:
        A_G - adjacency matrix of target graph (|V_G| x |V_G|)
        A_P - adjacency matrix of pattern graph (|V_P| x |V_P|)
    Output:
        True if subgraph isomorphism exists, else False

    Initialize M[i][j] = 1 if degree_A_P(i) ≤ degree_A_G(j) else 0
    return UllmannSearch(M, 0, A_G, A_P)


Procedure UllmannSearch(M, depth, A_G, A_P):
    if depth == |V_P|:
        if A_P ≤ M * A_G * Mᵀ:
            return True
        else:
            return False

    // Refine M using adjacency consistency
    Refine(M, A_G, A_P)

    for each column j in A_G where M[depth][j] == 1:
        M' = copy of M

        // Assign mapping for this row
        set all entries in row 'depth' of M' to 0
        M'[depth][j] = 1

        // Remove used column to maintain injectivity
        for i = 0 to |V_P|-1:
            M'[i][j] = 0 if i != depth

        if UllmannSearch(M', depth + 1, A_G, A_P):
            return True

    return False


Procedure Refine(M, A_G, A_P):
    repeat
        changed = false
        for each i in vertices of P:
            for each j in vertices of G:
                if M[i][j] == 1:
                    // Every neighbor of i must have some possible match among neighbors of j
                    supported = true
                    for each neighbor k of i in P:
                        hasSupport = false
                        for each neighbor l of j in G:
                            if M[k][l] == 1:
                                hasSupport = true
                                break
                        if not hasSupport:
                            supported = false
                            break
                    if not supported:
                        M[i][j] = 0
                        changed = true
    until not changed

Although the neighborhood heuristic prunes away many matrices, it still is not memory efficient. Indeed, we need to store a fresh copy of the matrix in case we need to backtrack to it.

VF2 Algorithm

Unlike Ullmann's Algorithm which relied on the matrix formulation, VF2 algorithm operates on a state space representation of the subgraph isomorphism problem. It performs a depth-first search on this state space.

Each node in this state space represents a partial injective mapping between pattern graph \(P\) and target graph \(G\). We start with an empty mapping state i.e no vertex is mapped between \(P\) and \(G\). At each step, we try to extend the current partial mapping by adding a single candidate node pair \((v_i, v_j)\).

State and frontier sets

  • Mapping: \(\mathrm{core}_P(u) = v\) if \(u\in P\) is currently mapped to \(v\in G\); \(\mathrm{core}_G(v) = u\) (inverse). Unmapped vertices have a special null value.
  • Frontier sets (undirected):
    • \(T^{P}\): vertices of \(P\) adjacent to already mapped vertices but not yet mapped.
    • \(T^{G}\): analogous set in \(G\).

Candidate selection

  • We pick the next pattern vertex \(u\) from \(T^{P}\) if it is non-empty, else any \(u \in V(P) \setminus \mathrm{mapped}_P\).
  • Build candidate targets \(v\) from \(T^{G}\), else any \(v \in V(G) \setminus \mathrm{mapped}_G\).
  • This focuses the search near the current boundary and reduces branching.

Feasibility Checks

Before adding a candidate pair \((u, v)\) to the mapping, VF2 performs feasibility checks to prune the search. A pair is feasible only if it satisfies these rules:

  1. Edge Consistency: For every already mapped neighbor \(u'\) of \(u\), its corresponding vertex \(v'\) in \(G\) must be a neighbor of \(v\). This ensures the local graph structure is preserved.

  2. Look-Ahead Pruning: The algorithm checks the number of neighbors of \(u\) and \(v\) that are in their respective "frontier" sets. The count for \(v\) must be at least as large as for \(u\). This prunes branches where the target graph lacks enough nodes to match the pattern's structure.

If a pair fails these checks, the algorithm backtracks, avoiding a fruitless search path.

Update and backtrack

  • On accepting a feasible pair \((u,v)\):
    • Set \(\mathrm{core}_P(u)=v\) and \(\mathrm{core}_G(v)=u\).
  • Move \(u\) and \(v\) out of frontier sets; insert their previously unseen neighbors into \(T^{P}\) and \(T^{G}\), respectively.
  • On failure, we simply need to backtrack to the previous state and restore the frontier sets (and any other state information). This is more efficient than restoring the entire matrix as in Ullmann's algorithm.

However, state management necessitates the use of multiple auxiliary data structures to maintain highly localized information about the search frontier. This increases the structural complexity compared to Ullmann's single matrix representation. But we are able to avoid matrix copying at every step of recursion. We are also able to perform better pruning at each stage due to these localized search frontier sets.

References

L. P. Cordella, P. Foggia, C. Sansone and M. Vento, "A (sub)graph isomorphism algorithm for matching large graphs," in IEEE Transactions on Pattern Analysis and Machine Intelligence

Wikipedia page

Ullmann's Algorithm

Technical Challenges of Indirect Control Flow