Introduction to DataFlow Analysis
Introduction
Dataflow analysis is a technique used in static analysis to gather information (of various kinds) about the program. This information can be used in multiple ways, such as performing optimizations, decompiling code, etc. In this post, we’ll break down the fundamentals of dataflow analysis and discuss how it is applied in modern compilers and software analysis tools.
A Motivating Example
Let us assume that given a program, we want to know what variables
are live at a point P in the program. A variable is
considered live at a point in the program if it holds a value that might
be read before the next write, i.e., if the value may be required at
some point in the future. This is called the Liveness
analysis and is crucial in determining optimal register/memory
allocation. It is also a classic example of a dataflow analysis.
Basics of Dataflow Analysis
It is helpful to start by imagining programs as a series of blocks that are connected by edges. Block1 is connected to Block2 if control flow can pass from Block1 to Block2. It is also possible to think of a program as a series of statements (instructions) executed sequentially; however, in most cases, the block-based representation is more useful.
Taking this one step further, we can imagine various kinds of information/data flowing in and out of these blocks. The block may or may not modify the information that enters it before passing it on to the successors of the block. Formally speaking, we define a function transfer and an operator join such that
\[ \textit{out}_b = \textit{trans}_b(\textit{in}_b) \]
\[ \textit{in}_b = \textit{combine}_{p \in \textit{pred}_b} (\textit{out}_p) \]
Intuitively, this just means that information flowing out of a block b can be expressed in terms of a function that takes as input the information flowing into b. The information flowing into b must be some combination of the information flowing out of all of the predecessors of b. It is clear that the transfer function and the combine operator vary depending on the kind of analysis we are performing.
It is also clear that this gives us information about the data flowing out of b, given that we know the data flowing into b. This is called forward dataflow analysis. We could also try to understand the data flowing into block b, given that we know the data flowing out of the block b. This is called backward dataflow analysis.
This works well for all blocks except the first block of the program, a.k.a. the entry block. By definition, it does not have any predecessor and hence no information flowing in. For the entry block, we must already know or assume the data (Boundary Condition). Once we do that, we can compute information at the start/end of any block, given that we have defined a transfer function and a combine operator.
Let us now discuss some important concepts related to dataflow analysis.
Abstract Interpretation
To understand Abstract Interpretation, think of two different types of semantics - Concrete Semantics and Abstract Semantics. Concrete semantics refer to the actual behavior of the program. However, computing this is not always feasible (see Rice's Theorem). Hence, we may choose another set (called an abstract domain) that over-approximates this concrete set. We can then track the behavior of the program with regard to the abstract set. Let us take some examples.
Sign Analysis
1 | |
Let us formally define some terms now. These definitions are taken from the book "Introduction to Static Analysis: An Abstract Interpretation Perspective".
Abstraction: We call abstraction a set A of logical
properties of program states, which are called abstract properties or
abstract elements. A set of abstract properties is called an abstract
domain
Concretization:Given an abstract element a of A, we call
concretization the set of concrete program states that satisfy it. We
denote it by γ(a)
Abstraction Function: A function α is called an
abstraction function if it maps an element x in the concrete set to an
element α(x) in the abstract set. That is, element α(x) is the
abstraction of x.
Best Abstraction: We say that a is the best abstraction
of the concrete set S if and only if S ⊆ γ(a) and for any a′ that is an
abstraction of S (i.e., S ⊆ γ(a′)), then a′ is a coarser abstraction
than a. If S has a best abstraction, then the best abstraction is
unique. When it is defined, we let α denote the function that maps any
concrete set of states into the best abstraction of that set of
states.
Abstract Interpretation is a broad framework that can be used to design a sound static analysis method.
Complete Lattice
In order to move further, it is important to understand the concept of a Complete Lattice. From Wikipedia
A complete lattice is a partially ordered set (L, ≤) such that every subset A of L has both a greatest lower bound (the infimum, or meet) and a least upper bound (the supremum, or join) in (L, ≤).
We are free to contrive an ordering of our choice as long as the ordering is Reflexive, Anti-Symmetric and Transitive in nature.
\[ x\leq x \]
\[ x \leq y \quad \text{and} \quad y \leq x \quad \Rightarrow \quad x = y \]
\[ x \leq y \quad \text{and} \quad y \leq z \quad \Rightarrow \quad x \leq z \]
Lattices are represented by Hasse's Diagrams
Abstract program states can be represented in the form of a complete lattice with a defined partial ordering. As an example suppose that we are interested in the value(values) that a variable of type int might hold at a particular point in the program. We can construct a lattice for all possibilities as follows (taken from Clang introduction to DataFlowAnalysis)
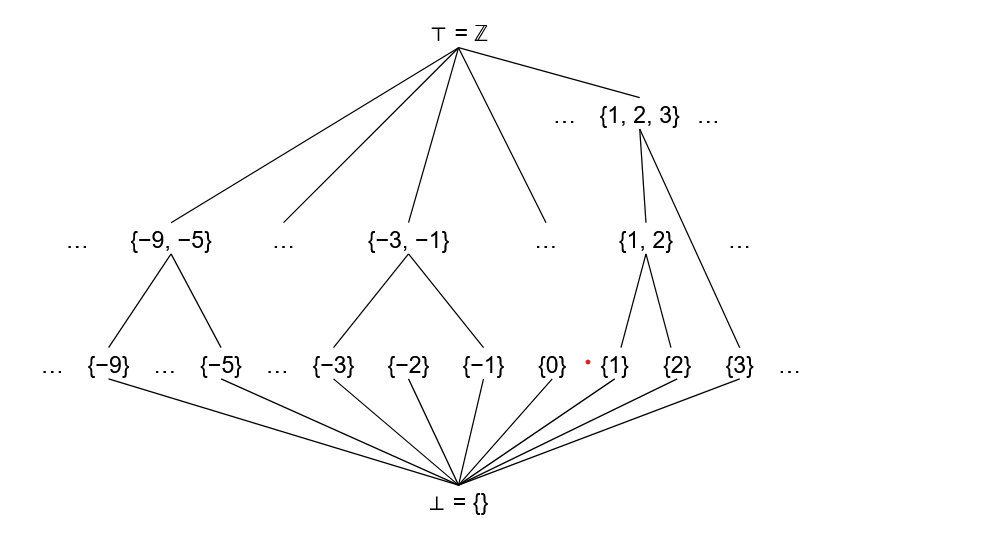
Here is how we can interpret this lattice. If a variable is only
initialized, we know nothing about its value. This is represented by the
bottom operator ⊥
If the variable is assigned a value, it must be an integer value. This is represented by all the sets containing a single integer as an element. If the value of a variable depends on condition such as
1 | |
This is represented by all the sets that contains two integers and so
on. Similarly, we have a set of integers taken three at a time and then
finally we have the Top T operator. The top operator simply
represents that we have too much information to feasibly track. In this
example, if the variable can have 4 or more values at a time, we
(arbitrarily) consider it too much information to track.
1 | |
For the above example lattice, how is the partial ordering defined?
\[ A \leq B \iff A \subseteq B \]
So far we have defined a unique lattice using domain of values and a partial ordering. Once we have defined a lattice, we can also define two operators - The Meet Operator and the Join Operator.
The meet operator operates on A and B to produce the
greatest lower bound (GLB) i.e the greatest set that is
less than or equal to both A and B
A partial ordering uniquely determines a meet operator and vice versa
\[ \texttt{Meet operator and partial ordering are related as follows} \]
\[ A \leq B \iff A \wedge B = A \]
where ^ denotes the meet operator. As an example, let us define a meet operator for our lattice for tracking variable values.
\[ A \leq B \iff A \subseteq B \]
\[ A \leq B \iff A \wedge B = A \]
It is easy to see that the Set Intersection operator is the meet operator for the defined lattice.
\[ A \leq B \iff A \cap B = A \]
The Join Operator, denoted by V produces the
least upper bound (LUB) i.e the least set that is greater
than or equal to both A and B
In our example of tracking possible variable value, the Join Operator is simply the Set Union Operator.
Fixed point and the Knaster–Tarski theorem
We are now ready to formalize dataflow analysis problems. To recap, we first decide on the domain of our values, depending on the problem at hand. Then, we construct a complete lattice L and define a partial ordering (and, consequently, a join operator and a meet operator). Then, we define a transfer function f:
\[ f: L \to L \]
A fixed point is a point x such that f(x)=x. To find such a fixed point for our dataflow analysis, we can use the fixed-point iteration algorithm. In the fixed-point iteration algorithm, we first initialize all the blocks, usually with ⊥ (no information). We then iterate over all the program blocks, applying their respective transfer functions to compute the data flowing out. We repeat this process until the data flowing out of all the blocks becomes constant. This is called the stable condition, and our analysis can safely terminate once we reach this fixed point.
How do we guarantee the existence of such a fixed/stable point? This is where the Knaster-Tarski theorem comes into play. The Knaster-Tarski theorem states the following:
\[ \texttt{Let } ((L, \preceq)) \texttt{ be a complete lattice.} \]
\[ \texttt{Let } ( f: L \to L ) \texttt{ be an increasing mapping.} \]
\[ \texttt {Let } F \texttt{ be the set (or class) of fixed points of } f : \]
\[ F = { x \in L \mid f(x) = x }. \]
\[ \texttt{Then } (F, \preceq) \texttt{ is a complete lattice.} \]
This means that a set of fixed points is guaranteed to exist (and to form a complete lattice) if the function f is monotonic. We conclude that if we choose our transfer function such that it is monotonic, our fixed-point iteration must converge to the fixed point.
However, there is a catch. Convergence is guaranteed only if the lattice has a finite height. The height of the lattice is defined as the length of the longest chain (totally ordered subset) from the bottom element (⊥) to the top element (⊤). However, as discussed earlier, we can arbitrarily choose a ⊤ element when we decide that we have too much information to track. This can truncate the height of a lattice from infinite to finite. (This is something we did when constructing the lattice for tracking variable values.)
Other techniques for dealing with infinite lattices include widening-narrowing, choosing a coarser abstraction, etc.
To complete our formalization, the family of transfer function (each block can have its own transfer function) selected must satisfy the following constraints in addition to being monotonic.
Identity function must be present.
\[ I(x) = x \in \mathcal{F} \]
\[ f, g \in \mathcal{F} \implies (f \circ g) \in \mathcal{F} \]
If each block has its own transfer function, the resulting transfer function can be composed as
\[ F(x) = f_1 \circ f_2 \circ f_3 \circ f_4 ...... \]
Reaching definitions
We will now look at a concrete example of dataflow analysis -
Reaching Definitions analysis. First we define a
Reaching Definition.
An assignment x=l reaches point P iff it does not get redefined/invalidated before P
A quick example just so we are clear
1 | |
First step is to define the domain of values.
\[ L = \mathcal{P}(\{ (x,s) \mid x \text{ is assigned at statement } s \}) \]
Next we define a lattice ordering as follows
\[ S_1 \sqsubseteq S_2 \quad \text{iff} \quad S_1 \subseteq S_2 \]
The join operator is Set Union and meet operator is Set Intersection
\[ \text{Join (Least Upper Bound):} \quad S_1 \vee S_2 = S_1 \cup S_2 \]
\[ \text{Meet (Greatest Lower Bound):} \quad S_1 \wedge S_2 = S_1 \cap S_2 \]
Now, we define our transfer function as follows:
\[ f(S) = (S \setminus \text{kill}) \cup \text{gen} \]
\[ \begin{aligned} where \\ S &\quad \text{is set of reaching definitions for block,} \\ \texttt{kill} &\quad \text{is set of definitions that is overwritten by block,} \\ \texttt{gen} &\quad \text{is set of new definitions introduced by block.} \end{aligned} \]
We remove all the definitions that are being redefined/invalidated in block B, and add all the new definitions introduced in block B to the set of definitions that is reaching the block B.
Hence we have the relation between Data In and Data Out as follows:
\[ \textit{out}_b = \textit{f}_b(\textit{in}_b) \]
We can easily verify that the above transfer function is monotonic. Note that kill and gen sets are fixed for a given block.
\[ \texttt{Let \( S_1, S_2 \) be two sets of reaching definitions such that:} \]
\[ S_1 \subseteq S_2 \]
Applying the transfer function:
\[ f(S_1) = (S_1 \setminus \text{kill}) \cup \text{gen} \]
\[ f(S_2) = (S_2 \setminus \text{kill}) \cup \text{gen} \]
\[ S_1 \setminus \text{kill} \subseteq S_2 \setminus \text{kill} \]
\[ (S_1 \setminus \text{kill}) \cup \text{gen} \subseteq (S_2 \setminus \text{kill}) \cup \text{gen} \]
which simplifies to:
\[ f(S_1) \subseteq f(S_2) \]
Thus, the transfer function f is monotonic.
What about the data flowing into B? Do we use the join operator, or the meet operator to combine the data flowing out from the predecessors of B? Consider the following example
1 | |
To ensure soundness, the analysis must assume that at P5 , both P2 and P4 are valid reaching definitions. Hence, we can conclude that the combine operator must be the join operator (Set Union).
\[ \textit{in}_b = \textit{join}_{p \in \textit{pred}_b} (\textit{out}_p) \]
Note: Reaching definition is of type
Forward DataFlow Analysis and May-Analysis. By
May-Analysis, we infer that a fact is true if it holds in any
predecessor. This is why we must use the join operator.
A Must-Analysis is an analysis in which a fact is true
if and only if it holds for all the predecessors. In this case, we would
use the meet operator to combine data flowing in from multiple
predecessors.
Now that we have defined concretely the transfer function and the combine operator, we only need to initialize each block (including the entry block) and iterate over each block, applying the respective transfer function, until the data flowing out of each block becomes constant. The analysis will conclude then.
Conclusion
We have seen that by leveraging the mathematics of complete lattice, monotonic functions and fixed-point iterations, we can analyze and track how information flows through a program. This enables us to modify, optimize and secure them.
Optimizations like dead-code elimination (removing unused code), constant propagation (replacing expressions with constant values), loop unrolling, all depend on the soundness of dataflow analysis. On the security front, dataflow analysis can be used to automate the detection of bugs like buffer overflows, integer overflow/underflow, command injections, etc.
PS: This was a summary of all that I have learnt about dataflow analysis. If you happen to spot a mistake, please reach out to me via X. Thanks a lot for reading!!
References
Books
- Principles of program analysis By Flemming Nielson
- Introduction to static analysis : An abstract interpretation perspective by Xavier Rival and Kwangkeun Yi
Others